Desde el punto de vista esotérico, la Conciencia (Luz) es la Correlación entre el Espíritu (Energía) y la Sustancia (Materia), o sea, E = mc², en la fórmula de Einstein.
Analógicamente, puede decirse que la Evolución de la Conciencia tiende hacia una simetría cada vez más perfecta entre el Espíritu y la Sustancia, hacia la proporción áurea entre ellos, a saber: hacia la Belleza del Ser.
En lo concerniente a la filosofía y la ciencia, he aquí algunos extractos del siguiente documento (solo en italiano) sobre el concepto de simetría entre el Uno y lo Múltiple, entre la Unidad y la Diferenciación (la numeración de las notas, los enlaces y las imágenes son de la redacción de TPS):
Simmetria e rottura di simmetria per comprendere il cambiamento. La tradizione del Timeo in Galileo e Keplero, de A. Briguglia
Simetría y conocimiento
(…) En Platón, la distancia del Uno, debida a la Díada, permanece oculta en las cosas percibidas, como una distancia del “modelo”, del que las cosas son imágenes. La simetría imperfecta —pero simetría al fin y al cabo— es lo que queda en las cosas como un recuerdo del Uno. ¿Qué puede unir dos cosas diferentes?: Es la sun-metría, es decir, la con-mensurabilidad.
En el Timeo aparece el término “sun-metría”, pero no es equivalente al término castellano ‘simetría’, más bien al término “analoghía”, que debería traducirse como “simetría”. Pero “analoghía” significa ‘proporción’. En la proporción, ya sea aritmética, geométrica o armónica, una media proporcional une dos cantidades; identifica lo que permanece invariable cuando se pasa de dos cantidades, en correlación entre sí, a otras dos.
En el Timeo, 31 C, Platón escribe que el más bello de los vínculos es el que convierte varias cosas en una. Y esto, por naturaleza, cumple la analoghía de la manera más bella.
La belleza está de por medio, comprendida como correspondencia entre las partes, semejanza, igualdad de relaciones, o sea: ¡Un acuerdo con un principio racional! Entre la proporción, la simetría y la belleza existe un círculo hermenéutico, dominado por el papel unificador de la analoghía.
El texto citado, en su totalidad, dice: «Pero no es posible que dos cosas se compongan bien por sí mismas, de una manera hermosa, prescindiendo de una tercera. De hecho, debe haber un vínculo de por medio que una uno con el otro. Y el más bello de los vínculos es el que de sí mismo y de las cosas vinculadas hace uno en grado supremo. Y esto, por naturaleza, cumple de la manera más hermosa la proporción (analoghía). Porque cuando de tres números, o masas, o potencias, cualesquiera que sean, el medio está al último como el primero está al medio; y además, a su vez, el medio está al primero como el último está al medio; entonces, el medio se convierte en el primero y el último; y el último y el primero se convierten en el medio; de esta manera, necesariamente, sucederá que todas las proporciones sean iguales, y, habiéndose convertido en lo mismo entre ellas, todas serán una unidad.» (Timeo, 31 C, 32 A)
En toda búsqueda de la simetría, para los antiguos y para los modernos, está implícita la misma preocupación, a saber: encontrar qué hace que un conjunto de elementos sean partes de un todo, conectados entre sí por relaciones matemáticas.
(…) Una simetría absoluta sería el dominio de lo idéntico, de lo no perceptible. Todo lo que percibimos es posible percibirlo porque se ha roto una simetría absoluta, de lo contrario no existiría nada definido, nada diferente. La simetría inicial permanece oculta en la multiplicidad de formas diferentes, en la que se puede romper la simetría.
(…) ¿Por qué causa placer el descubrimiento de la simetría? [1] Platón, retomado por Kepler, nos dice que esto depende de un proceso de reconocimiento y recuerdo del mundo de las ideas, que es favorecido por el papel dianoético de la geometría.
La idea de Platón fue retomada por Jung y Pauli con la teoría de los arquetipos. En sus comentarios sobre la obra de Kepler, Pauli escribe: «El proceso de comprensión de la naturaleza, así como la intensa felicidad que el ser humano experimenta al comprender, es decir, al tomar conciencia de una nueva verdad, parece basarse en una correspondencia, en la concordancia entre las imágenes internas preexistentes [arquetipos] en la psique humana y los objetos del mundo exterior con sus propiedades. Se sabe que esta teoría del conocimiento se remonta a Platón y es apoyada claramente por el propio Kepler.» [2]
La tradición helénica y la búsqueda del principio
En la historia del pensamiento occidental sobre la «naturaleza de las cosas» se han enfrentado dos tradiciones: la atomista, que se remonta a Leucipo y Demócrito, y la que ve lo idéntico que persiste en las transformaciones, no en las partículas materiales, sino en la estructura formal. Esta tradición, originada en la escuela de Pitágoras, a través del Timeo de Platón llegó a Galileo y Kepler en el siglo XVII.
En la actualidad, la teoría de los grupos de simetría parece aunar estas dos tradiciones, ya que la estructura algebraica de los grupos de transformaciones desempeña el papel formal de unificar las partículas fundamentales y sus interacciones.
A propósito de la escuela pitagórica, [Aristóteles] dice: «Primero se aplicaron a las matemáticas y las hicieron progresar y, nutridos por ellas, creyeron que los principios de estas eran principios de todos los seres. Y (…) pensaban que los elementos de los números eran elementos de todas las cosas, y que todo el ciclo era armonía y número. Y todas las concordancias que pudieron mostrar entre los números y los acordes musicales, entre los fenómenos y las partes del ciclo y entre todas las disposiciones del universo, las recogieron y ordenaron.»
(…) Con base en la intuición pitagórica se plantea el problema de la naturaleza del número, de la relación entre las formas geométricas, el número y el cosmos, de la «mente de Dios».
La Creación de Adán (de un fresco de Miguel Ángel)
Se sabe que la escuela pitagórica fue la que más atención prestó a los problemas de las escalas musicales. Ferguson ha seguido la historia de la relación entre la música, la física y la astronomía desde el siglo VI a. C., hasta la física del siglo XX. La correspondencia entre las correlaciones numéricas y los acordes musicales, empezando por el acorde de quinta, que iba a desempeñar un papel fundamental en el sistema del mundo de Kepler, les inspiró la idea de que detrás de las cosas había regularidades que podían expresarse mediante correlaciones entre los números enteros [racional: fracciones, N. de la R.]: «En el universo había orden, y este orden estaba formado por números. (…) Pitágoras y sus seguidores también habían descubierto que existía claramente un poderoso vínculo entre las percepciones de los sentidos humanos y los números que impregnaban y gobernaban todas las cosas. La naturaleza seguía una lógica fundamental, racional y bella; y los seres humanos estaban de acuerdo con ella, no solo en el nivel intelectual (podían descubrirla y comprenderla), sino también en el nivel sensorial (podían percibirla a través del oído en la música).»
(…) todavía no se ha reflexionado lo suficiente sobre cuánto influyeron las teorías musicales y el concepto de armonía en el nacimiento de la ciencia moderna en el siglo XVII: «Muchos historiadores de la ciencia, entre ellos Drake, señaló la brecha que surge por causa del descuido de la música como un componente fundamental que vincula los trabajos de la astronomía, la acústica, la óptica y la fisiología. De hecho, en aquellos años, científicos como Kepler, Mersenne, Galileo, Descartes, Huygens, Newton y Euler estuvieron involucrados profundamente en discusiones relacionadas con problemas clasificados como musicales, pero que luego se entrelazaron con las investigaciones que hoy nos parecen más directamente relacionadas con el desarrollo de la ciencia moderna. (…) De esta forma, la teoría musical se convirtió en el punto de encuentro entre el mundo abstracto de los números y la realidad física.» [Consultar el documento El Sonido Creador, N. de la R.]
La historia comienza con la escuela de Pitágoras y con el problema de identificar un término medio entre dos términos: aritmético, geométrico, armónico.
Las diferentes proporciones se escuchan luego por medio del monocordio. Con un trípode se trataba de dividir una cuerda en dos partes y decidir qué correlaciones entre las partes correspondían a un sonido agradable.
(…) El mismo Platón, en La República (Politeía) 336 D, señaló la necesidad de las matemáticas como entrenamiento de la mente que está en búsqueda de las formas; se dice que en la puerta de su Academia tenía grabado lo siguiente: «No entre nadie por mis puertas que no conozca la geometría.» Respecto a la geometría, Platón escribe: «La geometría es, en efecto, el conocimiento de lo que es eternamente.»
Cuando Platón regresó a Atenas, después de visitar al pitagórico Architas de Tarento en el año 389 a. C., adoptó un plan pitagórico de estudios para su Academia: aritmética, geometría, astronomía y música.
En el libro VII de La República, donde encontramos la famosa imagen de la caverna, el ascenso dianoético desde la doxa (opinión) hacia la episteme (conocimiento) y desde la eicasia (imaginación) hacia la noesis (perspicacia) y el posterior descenso hacia el gobierno del estado están descritos como un entrenamiento que requiere la ciencia del número (524 D, 526 C), la geometría plana (526 C, 527 C), la astronomía (527 D, 529 C), la ciencia de la armonía (529 C, 531 C).
La música de la que estamos hablando no es la práctica de «pulsar las cuerdas», sino la ciencia de las correlaciones numéricas. La ciencia de los armónicos está inextricablemente unida en el cuadrivio con las otras tres disciplinas. Pero, desde la perspectiva de Platón, todos ellos deben ser cultivados “en abstracto”. Por ejemplo, la astronomía debe estudiarse para resolver los problemas y no «mirando hacia arriba» (529 C).
(…) En el Timeo, Platón expuso su cosmología y transmitió a la tradición posterior la idea de que todo se rige por la simetría y por las correlaciones y proporciones. (…) se trata del origen del universo (cielo, planetas, hombre, animales) y su constitución. La materia, una realidad oscura e indeterminada, «el receptáculo de todo lo que se genera como una nutridora» (49A y 51A), está esperando ser dotada de un principio. El Demiurgo convence a la necesidad ciega, opuesta a la inteligencia, y que opera como una causa errante (πλανομενη αιτια, 48A) para conducir las cosas generadas hacia lo óptimo. Y lo óptimo es la impronta del Uno en lo múltiple, operado por las matemáticas, la forma intermedia entre el Uno y lo múltiple. [3]
Al principio reinaba el caos, «como ocurre cuando Dios está ausente; estas cosas que estaban en este estado las formó entonces (διεσκηματισατο) con formas y números (ειδεσι τε κατ αριτμοισ).» (53, B). El aire, el agua, la tierra y el fuego son realidades mutables y no pueden ser principios. Los principios son el triángulo rectángulo escaleno, la mitad del equilátero, a partir del que se puede formar el tetraedro (fuego), el octaedro (aire) y el icosaedro (agua) y el triángulo rectángulo isósceles, a partir del que se puede formar el cuadrado y el cubo (tierra). El dodecaedro no puede estar formado por triángulos, y representa el cosmos. La tierra no puede transformarse en aire, agua o fuego porque está formada por átomos geométricos diferentes. Los elementos se mantienen unidos por la proporción. Las cosas concretas no son ni aire, ni agua, ni fuego, ni tierra, sino una mezcla de ellos. De modo que no se puede decir «esto es fuego», sino «así es el fuego». Podemos decir, ¡este es el «modelo estándar», según Platón! Después de Platón, Euclides formalizó la teoría de las proporciones en el Libro V de sus Elementos (…).
En el Timeo, todas las partes se mantienen unidas por medio de la proporción. El alma del mundo, compuesta por la síntesis de lo Idéntico y lo Diferente, está estructurada en partes, según los números 1, 2, 3, 4, 8, 9, 27. Esta estructuración permite reconocer las proporciones en el mundo exterior. Otra subestructura conecta las partes a través de proporciones que reproducen los acordes de la escala pitagórica; la menor de ellas corresponde a sucesivas divisiones hasta 256/243, que es el semitono de la escala. La escala a la que se refiere Platón es la escala diatónica introducida por el pitagórico Filolao.
Kepler: La vía de las proporciones y la unidad del cosmos
Cuando se habla del papel de la simetría en la astronomía de Kepler, se piensa inmediatamente en los cinco poliedros regulares. En realidad, el papel de los sólidos platónicos en Kepler es cada vez más marginal, alusivo y simbólico, limitándose a determinar el número de planetas, mientras que otras simetrías, basadas en acordes armónicos, adquieren cada vez más el papel de la estructura de soporte del cosmos.
Con todas las debidas precauciones y distinciones, su uso de las simetrías guarda sorprendentes similitudes con su uso en la física de partículas. Al final de sus trabajos intensos, Kepler creyó haber encontrado, mediante una estructura formal, la manera de mantener unidos el número de planetas, las distancias de los planetas al sol y sus variaciones, los períodos de revolución, la densidad y las masas de los planetas, las dimensiones del cosmos (…) y, luego, la teología, el alma y la forma de gobierno.
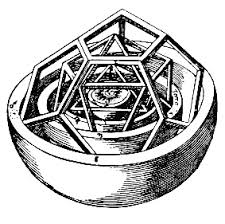
(…) La tradición de los cinco sólidos platónicos había encontrado un cuidadoso tratamiento en el Libro 13 de los Elementos de Euclides, que inspiró a Kepler. En 1509, Luca Pacioli (De Divina Proportione) dio testimonio del interés del Renacimiento por los sólidos platónicos. Leonardo da Vinci ilustrará la obra de Pacioli dibujándolos de forma transparente y resaltando su estructura. La innovación de Leonardo será retomada por Kepler en su Mysterium.
En la Dissertatio cum nuncio sidereo publicada en 1610, inmediatamente después de leer la Nuncius de Galileo, Kepler explicó las razones de su interés por la geometría y los poliedros regulares: «La geometría es una y eterna, brilla en la mente de Dios; y la participación que se le da a los hombres es una de las causas por las que el hombre es imagen de Dios. Bueno, en la geometría, después de la esfera, hay una familia de figuras que es la más perfecta de todas, la de los cinco sólidos euclidianos. Este mundo planetario nuestro está organizado precisamente de acuerdo con la regla y el modelo de estos sólidos.»
(…) Los únicos que acogieron el trabajo de Kepler fueron Galilei, entonces un desconocido matemático de Padua, y T. Brahe.
(…) La originalidad de la astronomía de Kepler, por la que se le puede considerar el primer astrofísico, consiste en algunas preguntas que otros astrónomos no se plantearon, por considerarlas disparatadas o sin respuesta; por ejemplo: ¿Por qué hay exactamente un número determinado de planetas? ¿Por qué están a una determinada distancia y con una determinada velocidad? ¿Qué les mueven?
A. Koyré escribe: «Kepler busca respuestas donde nadie más ve problemas». Para Copérnico, siguen siendo las esferas celestes las que hace girar a los planetas; para Bruno, son las animae; y Brahe se refugia en una actitud puramente calculadora. Según Koyré, la cuestión, de sabor puramente físico, tiene una raíz teológica. Kepler considera como unidad el Sol, las estrellas fijas y, fundamentalmente, el espacio intermedio. El Sol es la causa motriz; el espacio es el campo en el que se propagan estas fuerzas. La idea teológica es considerar los tres como un icono de la Trinidad: el Sol como icono del Padre, las Estrellas como icono del Hijo, el Espacio intermedio, el lugar de la creación, como un icono del Espíritu.
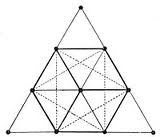(…) En el espacio, los sólidos del Timeo proporcionan la manera de determinar, de forma no arbitraria, el número de planetas. Así, este número se obtiene como resultado del hecho de que el cosmos está creado siguiendo ciertas simetrías.
(…) No es comprensible el júbilo de Kepler por haber encontrado precisamente en la correlación de la quinta armónica (3: 2) la ley que une las distancias y los tiempos de revolución si no se sigue esa larga tradición de investigadores (Pitágoras, Ptolomeo, Boecio, Giovanni Scoto Eriugena, Copérnico, etc.) que durante siglos habían escudriñado el movimiento de los planetas (distancias y velocidades) para encontrar las correlaciones armónicas.
Las correlaciones armónicas eran las invariantes que unían el cosmos al pasar de un planeta a otro. La búsqueda de las correlaciones armónicas estaba determinada por la idea de que debía existir una relación profunda entre el acorde armónico percibido (alma) y las correlaciones numéricas relativas a los planetas (cosmos), entre la música humana y la música del mundo.
Para Galileo, las órbitas elípticas rompen la simetría del cosmos; para Kepler son el camino para descubrir simetrías más profundas que consisten en correlaciones y proporciones, todas ellas generadas por la correlación de quintas armónicas. (…) [Pero incluso] cuando Kepler renunció a las órbitas circulares, el arquetipo del círculo y la esfera siguieron siendo fundamental. Después de todo, el cosmos de Kepler continúa siendo esférico. Dios, el alma y el cosmos son comprensibles a través de un único arquetipo. Cuando se perciben los rayos de los planetas procedentes de los ángulos adecuados, en el alma suenan como consonantes.
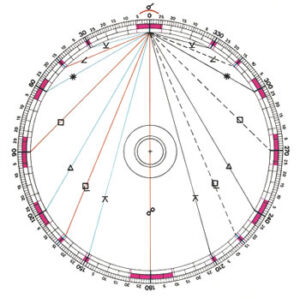Los ángulos apropiados son los relativos a los polígonos regulares inscritos en el círculo; el posicionamiento de los planetas para ser observados bajo estos ángulos constituye un «aspecto». De las correlaciones que se pueden combinar con los lados (por ejemplo, la correlación de quinta, 3/2, con el pentágono [¿o con el Triángulo y el 3.er Rayo?, N. de la R.]) surgen los acordes consonantes de la escala pitagórica.
(…) El proyecto de Platón de reducir los muchos al uno no le lleva hacia el atomismo. Del Mysterium a las Harmonices —el hilo conductor hacia la unidad que le llevará al descubrimiento de las tres leyes y a lograr «la derrota del circularismo»— es la búsqueda de la explicación física del mundo, su estructura armónica.
Incluso cuando Kepler buscó en la Strena seu de nive sexangula (1611) la causa de la simetría hexagonal de la nieve, no recurrió a la estructura atómica, sino a las razones formales de eficiencia de superficie-volumen.
Son los motivos formales los que hacen que el hombre y el mundo armonicen de la misma manera [sustituiríamos los motivos formales por los funcionales, en el sentido de que la forma está determinada por su función en el todo, que a su vez depende del principio/arquetipo subyacente, N. de la R.]. La proporción en las distancias y en las velocidades de los planetas es tal que es reconocida por la mente humana, que lleva dichas proporciones como arquetipos.
Las órbitas elípticas son el resultado de la necesidad física y de las leyes de la armonía.
Si queremos construir el mundo según las leyes de la armonía, no bastan los sólidos regulares, que darían órbitas circulares concéntricas y velocidades constantes; las proporciones armónicas obligan al Creador a variar las velocidades de los planetas. (…) En síntesis: los datos astronómicos (1) + la armonía (2) + la necesidad física (3) = las órbitas elípticas. Los sólidos platónicos, después de las observaciones de Brahe, solo tienen la tarea de fijar el número de planetas [hasta Saturno, N. de la R.].
(…) Para construir la armonía cósmica, Kepler parte de Saturno, para el que tenemos un acorde de tercera mayor entre el afelio y el perihelio. Partiendo del tono sol [4], el acorde será sol – si. Para construir las melodías de los demás planetas, es necesario dividir las velocidades angulares por dos [reducción de octava para la longitud de onda, elevación de octava para la frecuencia, N. de la R.] hasta obtener tonos en la misma octava de Saturno. Por ejemplo, si en el afelio dividimos la velocidad angular de la Tierra por 2, cinco veces, obtenemos 1′ 47″, próximo a la velocidad de Saturno en el afelio. La melodía de la Tierra también comenzará con un sol, cinco octavas por encima de la de Saturno. (…) El acorde entre los planetas debe construirse a partir de sol monotono [un único tono] de la Tierra y el mi – mib de Venus [una tercera]. Las órbitas elípticas y las velocidades variables revelan simetrías más profundas y ocultas que vinculan la astronomía y la música; se trata de simetrías dinámicas en contraposición a las estáticas, que están vinculadas a la forma geométrica.
El hecho es que aún no se conoce la relación entre el tiempo de revolución y la distancia. Si se conociera, se podría, partiendo de los tiempos, es decir, de la armonía, encontrar las distancias. Es una relación que Kepler la buscó más o menos durante dos décadas, que le costó 17 años de intentos sobre los datos de Brahe, y que finalmente apareció en su mente el 15 de mayo de 1618: «Es una cosa muy cierta y exacta que los tiempos periódicos de dos planetas cualesquiera están precisamente en la proporción sesquiáltera de sus distancias medias, o sea, de sus órbitas». Es decir, T1²/ T2² = R1³/ R2³.
En este punto, partiendo de los tiempos de revolución, Kepler estableció en 1000 la distancia media de la Tierra al Sol, obtuvo el semieje mayor y la excentricidad de cada planeta y los comparó con los datos de Brahe. «La teoría armónica salió victoriosa de la confrontación con los hechos.»
El largo camino, de veinticuatro años, que le llevó de la materialidad de la forma a la armonía, del Mysterium a las Harmonices, está descrito por Kepler en el libro quinto de esta última obra: «La proporción que los sólidos regulares habrían prescrito para los orbes planetarios, al ser inferior y referirse solo al cuerpo y a la materia, debía ceder ante las armonías de lo necesario para que pudieran aproximarse y contribuir a la belleza de los movimientos de los globos.»
El Harmonice es la continuación del Mysterium, el apogeo de una obsesión de toda la vida. Aquí Kepler intentaba, sencillamente, desentrañar el secreto fundamental del universo ofreciendo una vasta síntesis de geometría, música, astrología, astronomía y epistemología. Era algo que nadie había intentado desde la época de Platón, y nadie lo ha intentado desde entonces. Después de Kepler se produce de nuevo la fragmentación de la experiencia; la ciencia se separa de la religión; la religión, del arte; la sustancia, de la forma; la materia, del espíritu.
(…) Los físicos de partículas han asumido el sueño de una unificación en la que las teorías tuvieran menos constantes injustificadas. En la historia de la comprensión de las interacciones fuertes, casi se tiene la impresión de que los físicos, en algún momento, se han preocupado por elaborar teorías simples y elegantes siguiendo el hilo de la simetría, y las han estudiado incluso cuando estaban claramente en desacuerdo con los datos experimentales; estaban animados por la confianza de que el número y las masas de las partículas deberían responder a una lógica, en la que la belleza debería jugar un papel. La teoría del Campo de Yang-Mills era buena, pero sus predicciones parecían contradecir el hecho de que los bosones de la interacción débil debían tener masa. Había que inventar un mecanismo para romper la simetría. Un río kárstico fluía bajo un enfoque puramente fenomenológico a la espera de poder resurgir. Y cuando resurgió, tenía todas las características del programa de Kepler, a saber: explicar el variopinto mundo de las interacciones fundamentales con estructuras unificadoras.
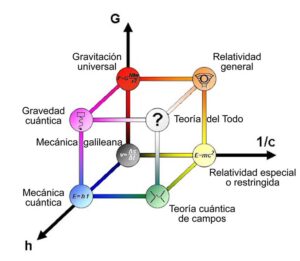Desde los filósofos jónicos hasta nuestros días, la idea de que la naturaleza sea comprensible, que sea un libro, que la complicación del devenir y de los niveles de la realidad respondan a restricciones simples y elegantes en un nivel fundamental, siempre han acompañado las investigaciones.
(…) La historia del modelo estándar [5] es la conclusión de un largo recorrido, que comenzó en el siglo XX con Einstein, Heisenberg, Noether, Weyl, Yang y Mills: «Con la comprensión de la ruptura espontánea de la simetría, las diferentes contribuciones acabaron confluyendo en la “Standard Theory”. Este fue el retorno de aquellos que creían en la belleza y perfección de las leyes fundamentales de la física.» Quizás también fue la venganza de Kepler.
Modelo estándar de las partículas elementales
Este retorno ha reavivado, de forma más acuciante, un problema que tiene una larga tradición a sus espaldas: el del papel de las matemáticas en la comprensión de la naturaleza y de la física en particular. La ley de la naturaleza formalizada algebraicamente es el objeto que mantiene unidos fenómenos dispares en un campo determinado. La simetría es el vínculo al que se somete o debe someterse la ley si se utiliza la simetría como un a priori heurístico. La simetría está definida por el conjunto de transformaciones que puede sufrir la ecuación que formaliza la ley, de modo que siga siendo covariante.
Pero, ¿cuál es el significado filosófico de todo esto? El problema de Wigner —a saber: «Cuál es la razón de la eficacia de las matemáticas en la física»— es, como hemos visto, muy antiguo y se le ha dado la vuelta una y otra vez en innumerables ocasiones.
(…) Si nos quedamos en el siglo XVII podemos decir que Galileo, Kepler, Descartes, Boyle, Newton tenían ideas diferentes sobre el papel de la simetría en las leyes de la naturaleza. Pero todo el mundo se ha planteado el problema de forma explícita o implícita. Todos ellos, de diferentes maneras, compartían la idea cristiana [más generalmente, de todas las tradiciones espirituales, N. de la R.] de que un mundo creado por el Logos solo podía ser inteligible.
La moderna física de partículas ha agravado el problema de la eficacia de las matemáticas en la física, ya que toma el requisito de la simetría como un ganador a priori heurístico y metodológico (…) (!). A partir de 1905, una ley científica solo puede ser aceptada si goza de invariancia en un determinado grupo de transformaciones. De hecho, la ley suprema parece serlo: toda ley física debe ser covariante.
Pero, ¿cuál es el valor realista de las simetrías ocultas, dado que no son accesibles empíricamente, sino que solo lo son los fenómenos resultantes de la ruptura de la simetría oculta? ¿De dónde proviene la asimetría de los estados si la estructura es simétrica?
(…) Además de las preguntas ya formuladas, hay otra: ¿Puede una sola teoría física dar cuenta de todos los fenómenos? Hay dos aspiraciones marcadas en el sentimiento colectivo: la aspiración a una imagen unitaria del mundo y la que lleva, en cambio, a marcar las diversidades o incluso las diferencias. [6]
¿Es el libro de la naturaleza realmente un libro? Boyle, en “El cristiano virtuoso”, está seguro: «El libro de la naturaleza es un gran y bello tapiz enrollado que no podemos ver todo de una vez, sino que debemos contentarnos con esperar el descubrimiento de su belleza y simetría poco a poco.» ¡Como Galileo, Kepler, Newton!
(…) Volviendo a las consideraciones de Wigner, nos confrontamos entonces con problemas y misterios; estos últimos parecen difíciles de ser manejados por cualquier teoría filosófica. Pero nos enfrentamos a problemas y misterios que, en lugar de empobrecer o inducir a la frustración, nos conducen paradójicamente al sentido de la vida y de la investigación. (…) «El sentido pleno de la vida, el sentido colectivo de todos los deseos humanos, es fundamentalmente un misterio que escapa a nuestra comprensión. Cuando era joven me irritaba esta situación; pero ahora he hecho las paces con ello. También siento un cierto honor por estar asociado con un tal misterio.»
El principio y el final se espejan el uno en el otro, por eso coinciden.
El ritmo que los une vive en el Espacio,
donde todo lo que se duplica se vuelve a unir.
Una ley preside secretamente la libertad sin obstaculizarla:
Es la ley de la simetría proporcional,
que gobierna lo que va del Altísimo al Abismo, y los iguala.
*
Yo estoy en el Centro y soy el Centro en todas partes.
Determino los puntos de partida y de llegada.
Así creo la Belleza, que es el signo de la unión.
(Ritual de Capricornio, 4.o Aspecto)
(Este artículo aparece en correspondencia con la importante alineación Tierra-Venus-Sol, una de las cinco que trazan la estrella de cinco puntas de su correlación mutua en el cielo cada 8 años).
[1] Sin embargo, la simetría perfecta también causa incomodidad. Siempre es necesario que un elemento de ruptura, incluso oculto, aproxime la simetría a la vida. Numerosos autores relatan en diferentes variantes la idea de que la introducción de elementos asimétricos en tapices o mosaicos se hizo a propósito para no despertar la ira de los dioses. Thomas Mann, en un famoso pasaje de La Montaña Mágica, hace que el protagonista, perdido en una tormenta de nieve, perciba algo mortal en la “gélida regularidad”, “hostil a la vida”, de cada copo de nieve, junto con la alegría de inventar la naturaleza, ya que cada copo era diferente a los demás.
[2] Pauli, al final de su trabajo sobre Kepler, observó (esto fue en 1952) que los científicos habían perdido la imagen unitaria del mundo y se preguntaba si era posible recuperarla. Sin embargo, la condición para la recuperación era que las ciencias naturales aceptaran que solo eran una parte de esta imagen. [Consultar el documento La Manifestación, N. de la R.]
[3] Dijksterhuis comenta (p. 27-28): «Todo el espíritu del Timeo es diametralmente opuesto a la imagen del mundo de los atomistas. Según la opinión de estos, tanto la génesis del universo como los acontecimientos que en él tienen lugar permanecen sujetos al azar ciego, mientras que en el Timeo un Demiurgo benevolente y sabio transforma el caos en un cosmos ordenado. Mientras que los atomistas consideraban la vida de los dioses y de los hombres como un caso especial de la movilidad universal de los átomos, Platón hace del mundo un ser vivo dotando al cuerpo del mundo de un alma del mundo; mientras que los atomistas no tenían ninguna respuesta que dar a los problemas de la existencia del universo y de su finalidad, el Timeo explica ambas cosas: la bondad del Demiurgo no podía permitir el caos, y le indujo a transformar la materia espacial caótica en un conjunto armonioso y equilibrado, que debía ser semejante a Él, lo más posible.»
[4] Considerada entonces como la nota inicial de las escalas musicales e indicadas por la letra gamma γ, que también indicaba el punto de intersección entre la eclíptica y el ecuador celeste, el origen del sistema de referencia para calcular la posición de los astros en el cielo.
[5] «El Modelo Estándar incluye una serie de parámetros arbitrarios (una veintena); y en el estado actual de los conocimientos, la teoría sería matemáticamente consistente con cualquier valor de estos parámetros, al menos dentro de unos límites bastante amplios. Algunos de estos parámetros determinan, de forma continua, cómo se rompen las simetrías del Modelo Estándar. Cada una de estas realizaciones daría lugar a Universos diferentes, igualmente consistentes, con una amplia gama de propiedades físicas y diferentes modos de evolución.» (Maiani in Battimelli, p.57).
[6] Una vez más, Platón y Aristóteles se enfrentan. Por un lado, la aspiración de reconducir todo a una matriz común: el Uno; por otro, la defensa de la autonomía de los seres, de su diversidad irreductible, de su no deducibilidad desde una base de reducción. El reduccionismo y el antirreduccionismo, la atención a las partes y al todo, el atomismo y la identificación de la sustancia, entendida en el sentido aristotélico, como entidad a la que se atribuye la existencia en sentido propio, son tendencias que encontramos entre los físicos, aunque prevalezca una filosofía reduccionista.»
Nota: Este artículo ha sido traducido del original en italiano; consultar aquí.